방학동안 학회에서 김성훈 교수님의 PyTorch Zero To All 강의로 공부를 하게 된 김에 스스로 정리해보려고 합니다.
좋은 강의 공유해주신 김성훈 교수님께 감사드립니다.
강의링크:
https://www.youtube.com/playlist?list=PLlMkM4tgfjnJ3I-dbhO9JTw7gNty6o_2m
PyTorchZeroToAll (in English)
Basic ML/DL lectures using PyTorch in English.
www.youtube.com
Linear Model
저희는 input x를 받아 output y를 예측하는 모델을 만들고자 합니다. 이번 강의에서는 그 모델이 linear model인 경우에 대해서 다루고 있습니다. Linear model, 즉 선형 모델이란 모수와 타깃변수의 관계가 선형인 모델을 의미합니다. 일반적으로 선형 모델은 y = x * w + b의 꼴로 표현합니다. 여기서 w = weight(가중치)(=모수)를 뜻하고 b = bias(편향)을 나타냅니다. 설명의 편의를 위해 bias를 drop한 $\hat{y}$ = x * w을 살펴보겠습니다.
불행히도 우리는 데이터에 대한 아무런 인사이트도 가지고 있지 않기 때문에 w = random value로 탐색을 시작하게 됩니다.
목표는 실제값인 파란 선에 최대한 가까운 예측을 하는 것입니다. 이 가까움의 척도로 활용되는 것이 error = $\pmb{(\hat{y} - y)^2}$입니다. 다시, 목표는 이 error 값을 최소화하는 $\hat{y}$를 찾는 것이 됩니다.

예제 1) w = 3인 경우
| Hours, x | Points, y | Prediction $\hat{y} = x * w$ | loss = $(\hat{y} - y)^2$ |
| 1 | 2 | 3 | 1 |
| 2 | 4 | 6 | 4 |
| 3 | 6 | 9 | 9 |
이 때, 각 run에서의 loss를 모두 취해 데이터 전체의 loss를 평가하기 위해 loss들의 평균인 MSE를 사용합니다. MSE를 수식으로 나타내면 다음과 같습니다.
MSE = $\frac{1}{N} \sum_{n=1}^{N} (\hat{y_n} - y_n)^2$
예제 1의 경우 MSE = $\frac{1 + 4 + 9}{3} = \frac{14}{3}$입니다.
예제 2) w = 2인 경우
| Hours, x | Points, y | Prediction $\hat{y} = x * w$ | loss = $(\hat{y} - y)^2$ |
| 1 | 2 | 2 | 0 |
| 2 | 4 | 4 | 0 |
| 3 | 6 | 6 | 0 |
예제 2의 경우 MSE = 0으로, 실제로 이런 일이 일어날 확률은 매우 희박하지만 저희의 예제의 경우에서는 가장 이상적인 경우라고 할 수 있습니다. 에러를 최소화하는 $\hat{y}$, 즉 최적의 w값을 찾은 경우입니다.
import numpy as np
import matplotlib.pyplot as plt
#실습에 필요한 library를 import합니다.
x_data = [1.0, 2.0, 3.0]
y_data = [2.0, 4.0, 6.0]
#실습에 필요한 데이터셋을 정의합니다.
# our model for the forward pass
def forward(x):
return x * w
#y_hat값인 x * w, x_data와 weight을 곱해주는 함수 forward를 정의합니다.
# Loss function
def loss(x, y):
y_pred = forward(x)
return (y_pred - y) * (y_pred - y)
#error인 (y_hat - y)^2를 계산해주는 함수 loss를 정의합니다.
# List of weights/Mean square Error (Mse) for each input
w_list = []
mse_list = []
#나중에 그릴 그래프를 위해 공백리스트를 만들고 순서에 맞는 w값과 mse값을 append
#0부터 4까지 0.1 간격으로 for loop 구현
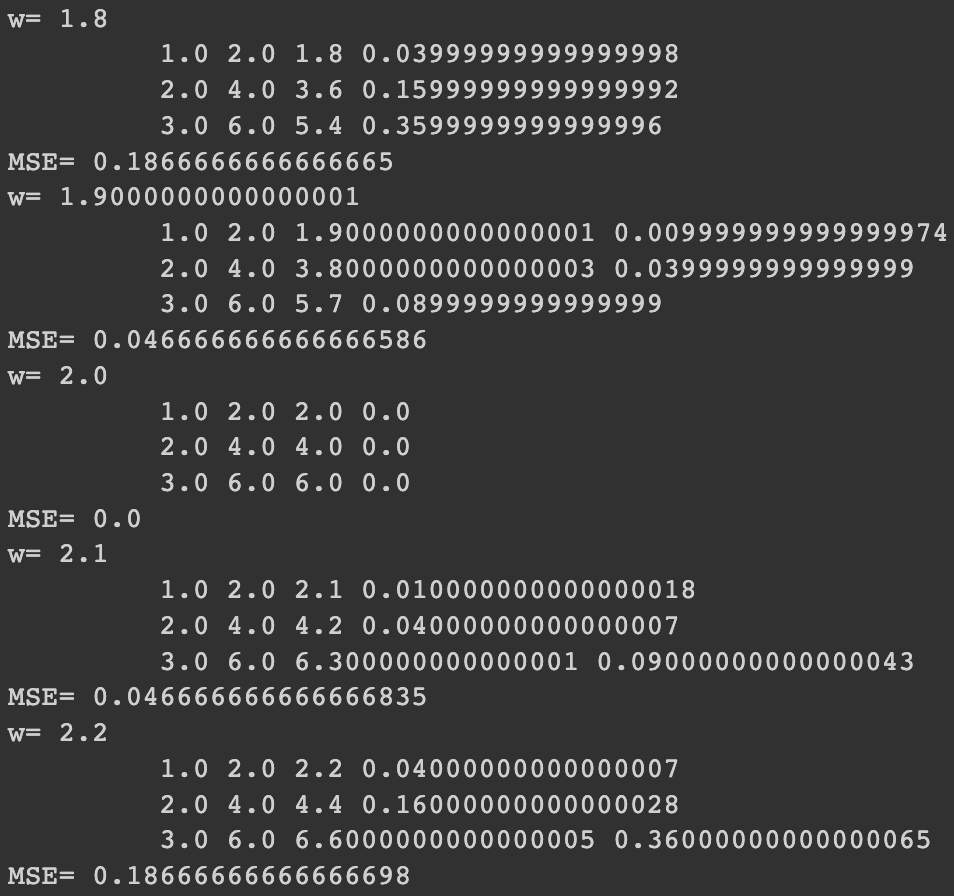
for w in np.arange(0.0, 4.1, 0.1):
# Print the weights and initialize the lost
print("w=", w)
l_sum = 0
#zip함수는 양 데이터를 하나씩 차례로 짝을 지어줌
for x_val, y_val in zip(x_data, y_data):
# For each input and output, calculate y_hat
# Compute the total loss and add to the total error
y_pred_val = forward(x_val)
l = loss(x_val, y_val)
l_sum += l
print("\t", x_val, y_val, y_pred_val, l)
# Now compute the Mean squared error (mse) of each
# Aggregate the weight/mse from this run
print("MSE=", l_sum / len(x_data))
w_list.append(w)
mse_list.append(l_sum / len(x_data))
#x_data와 y_data에서 값을 하나씩 뽑아 loss를 계산, 계산한 loss를 l_sum에 저장해 mse를 구하는데 사용
#이를 w가 0일 때, 0,1일 때, 0.2일 때부터 4일 때까지 반복, 아까 정의한 공백리스트 w_list와 mse_list에
#w값과 mse값 각각 저장
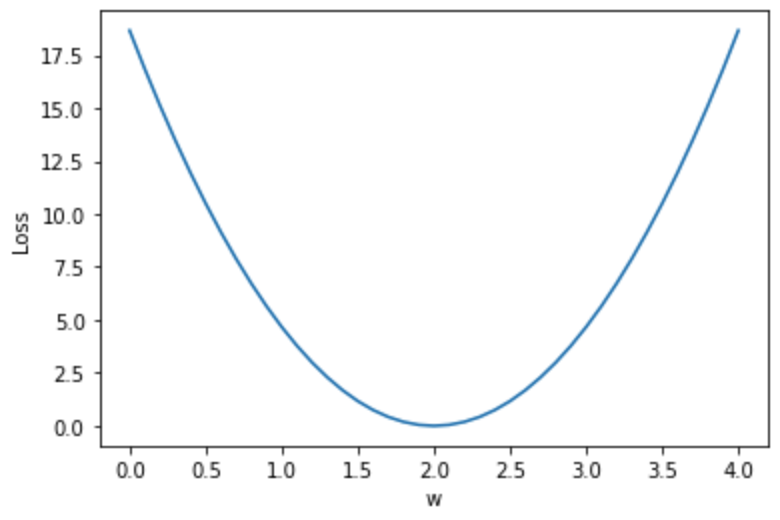
# Plot it all
plt.plot(w_list, mse_list)
plt.ylabel('Loss')
plt.xlabel('w')
plt.show()
#위에서 얻은 값들을 이용하여 loss를 시각화
실행 결과를 통해서도 w = 2.0인 경우가 MSE값이 앞서 살펴본 것과 마찬가지로 0인 이상적인 경우라는 것을 확인할 수 있습니다.
'ML \ DL > PyTorch Zero To All' 카테고리의 다른 글
| PyTorch Lecture 10: Basic CNN (0) | 2022.07.26 |
|---|---|
| PyTorch Lecture 09: Softmax Classifier (0) | 2022.07.14 |
| PyTorch Lecture 06: Logistic Regression (0) | 2022.07.13 |
| Pytorch Lecture 04: Back-Propagation and Autograd (0) | 2022.07.13 |
| PyTorch Lecture 03: Gradient Descent (0) | 2022.07.13 |