방학동안 학회에서 김성훈 교수님의 PyTorch Zero To All 강의로 공부를 하게 된 김에 스스로 정리해보려고 합니다.
좋은 강의 공유해주신 김성훈 교수님께 감사드립니다.
강의링크:
https://www.youtube.com/playlist?list=PLlMkM4tgfjnJ3I-dbhO9JTw7gNty6o_2m
PyTorchZeroToAll (in English)
Basic ML/DL lectures using PyTorch in English.
www.youtube.com
Logistic Regression
이전까지는 저희는 input x를 제공받아 linear opearation을 거쳐 output y를 출력해내는 linear model들에 대해서 다루었습니다. 이 때, input값, output값 모두 실수였습니다. 하지만 실생활에서는 output으로 0과 1 2개의 value만을 가지는 binary prediction이 매우 유용하고 잘 쓰입니다. 단순한 예로는 축구경기에서 이길지 질지를 예측하는 등의 문제가 있습니다.
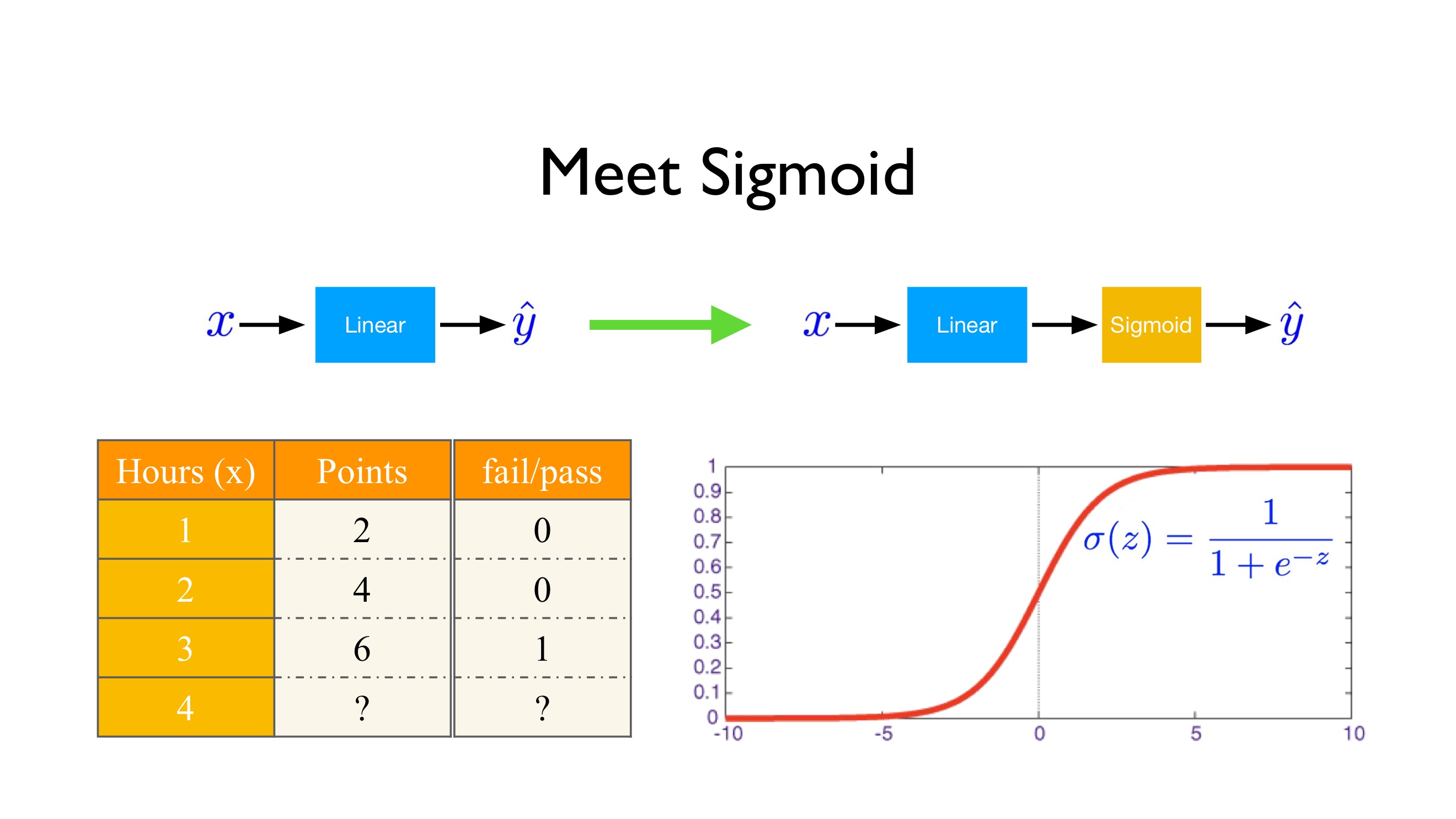
우리의 모델이 실수가 아닌 0, 1값을 예측하게 하는 방법 중에 하나는 sigmoid 함수를 사용하는 것입니다.
x -> linear -> sigmoid -> $\pmb{\hat{y}}$
sigmoid 함수는 $\delta(z) = \frac{1}{1+e^{-z}}$로 정의되고 모양은 아래 그림과 같습니다. sigmoid함수는 언제나 0과 1 사이의 값만을 지닙니다.
sigmoid 연산을 거친 $\hat{y}$ > 0.5 라면 1로 예측을 하고, $\hat{y}$ < 0.5 라면 0으로 예측합니다.
sigmoid함수라는 새로운 함수를 사용했기 때문에, 기존에 사용했던 MSE는 사용하지 못하고 Cross Entropy Loss라는 새로운 loss를 사용합니다. Cross Entropy Loss는 다음과 같습니다.
loss = $-\frac{1}{N} \sum_{n=1}^{N}y_nlog \hat{y_n} + (1 - y_n)log(1-\hat{y_n})$
| y | y_pred | loss |
| 1 | 0.2 | -1log0.2 $\approx$ 0.7 |
| 1 | 0.8 | -1log0.8 $\approx$ 0.1 |
| 0 | 0.1 | -1log0.9 $\approx$ 0.05 |
| 0 | 0.9 | -1log0.1 $\approx$ 1 |
from torch import tensor
from torch import nn
from torch import sigmoid
import torch.nn.functional as F
import torch.optim as optim
# Training data and ground truth
x_data = tensor([[1.0], [2.0], [3.0], [4.0]])
y_data = tensor([[0.], [0.], [1.], [1.]])
#사용할 데이터를 준비해줍니다. 데이터는 3x1의 tensor로, 각 x와 y데이터가 짝을 이룹니다.
#1. Design your model using class with Variables
#nn.Module의 subclass인 class Model을 생성해줍니다.
class Model(nn.Module):
def __init__(self):
"""
In the constructor we instantiate nn.Linear module
"""
super(Model, self).__init__()
#subclass인 Model이 부모클래스 nn.Module의 속성을 가지고 초기화됩니다.
self.linear = nn.Linear(1, 1) # One in and one out
#torch.nn.Linear를 이용하여 1개의 input을 받아 1개의 output을 뱉는 linear model을 생성합니다.
def forward(self, x):
"""
In the forward function we accept a Variable of input data and we must return
a Variable of output data.
"""
y_pred = sigmoid(self.linear(x))
return y_pred
#self.linear에 sigmoid함수를 씌워줘 y_pred값이 0과 1 사이의 값을 가지게 합니다.
#forward() 함수는 모델이 학습데이터를 입력받아서 forward 연산을 진행시키는 함수입니다.
#forward() 함수는 모델 객체를 데이터와 함께 호출하면 자동으로 실행됩니다.
#예를 들어 model(데이터)와 같은 형식으로 객체를 호출하면 자동으로 forward 연산이 수행됩니다.
# our model
model = Model()
#정의한 class Model에 대해 객체 model을 생성합니다.
#2. Construct loss and optimizer(select from PyTorch API)
# Construct our loss function and an Optimizer. The call to model.parameters()
# in the SGD constructor will contain the learnable parameters of the two
# nn.Linear modules which are members of the model.
criterion = nn.BCELoss(reduction='mean')
#기존에 사용했던 binary cross entropy loss를 torch.nn.BCELoss로 불러와 사용합니다.
#reduction = 'mean'이면 설명에 사용했던 대로 loss들의 평균을 사용하지만 reduction = 'sum'인 경우
#loss들의 총합을 사용합니다..
optimizer = optim.SGD(model.parameters(), lr=0.01)
#model.parameters()가 업데이트를 필요로 하는 모든 variable들을 SGD함수에 제공해줍니다.
#learning rate는 0.01입니다.
#3. Training: forward, loss, backward, step(update)
# Training loop
#0부터 999까지 1000번
for epoch in range(1000):
# Forward pass: Compute predicted y by passing x to the model
y_pred = model(x_data)
# Compute and print loss
loss = criterion(y_pred, y_data)
print(f'Epoch {epoch + 1}/1000 | Loss: {loss.item():.4f}')
# Zero gradients, perform a backward pass, and update the weights.
optimizer.zero_grad()
#backward()를 사용하여 gradient를 구하기 전에 gradient를 모두 0으로 초기화합니다.
loss.backward()
#backward propagation을 사용하여 필요한 모든 variable(model.parameters())에
#대해 gradient 구합니다.
optimizer.step()
#마찬가지로 model.parameters()를 gradient를 이용하여 update 해줍니다.
#w.data = w.data - 0.01 * w.grad.data와 동일한 기능
# After training
print(f'\nLet\'s predict the hours need to score above 50%\n{"=" * 50}')
hour_var = model(tensor([[1.0]]))
print(f'Prediction after 1 hour of training: {hour_var.item():.4f} | Above 50%: {hour_var.item() > 0.5}')
hour_var = model(tensor([[7.0]]))
print(f'Prediction after 7 hours of training: {hour_var.item():.4f} | Above 50%: { hour_var.item() > 0.5}')
#0.5가 넘으면 True, 넘지 못하면 False가 나오게끔 세팅해줍니다.
#공부를 1시간 했을 경우 50점을 넘지 못했기 때문에 False를 출력하고 7시간 한 경우는 50점을 넘겼기 때문에 True를 출력합니다.
'ML \ DL > PyTorch Zero To All' 카테고리의 다른 글
| PyTorch Lecture 10: Basic CNN (0) | 2022.07.26 |
|---|---|
| PyTorch Lecture 09: Softmax Classifier (0) | 2022.07.14 |
| Pytorch Lecture 04: Back-Propagation and Autograd (0) | 2022.07.13 |
| PyTorch Lecture 03: Gradient Descent (0) | 2022.07.13 |
| PyTorch Lecture 02: Linear Model (0) | 2022.07.13 |