방학동안 학회에서 김성훈 교수님의 PyTorch Zero To All 강의로 공부를 하게 된 김에 스스로 정리해보려고 합니다.
좋은 강의 공유해주신 김성훈 교수님께 감사드립니다.
강의링크:
https://www.youtube.com/playlist?list=PLlMkM4tgfjnJ3I-dbhO9JTw7gNty6o_2m
PyTorchZeroToAll (in English)
Basic ML/DL lectures using PyTorch in English.
www.youtube.com
Softmax Classifier

다음과 같은 image dataset을 각각 0부터 9까지 10개의 label에 분류하기 위해서는 이전에 배웠던 bianary classifier인 logistic regression만으로는 부족합니다. 각 label에 속할 확률이 어떻게 되는지를 나타내는 10개의 output을 갖는 경우를 생각하는 것이 더 자연스럽습니다.
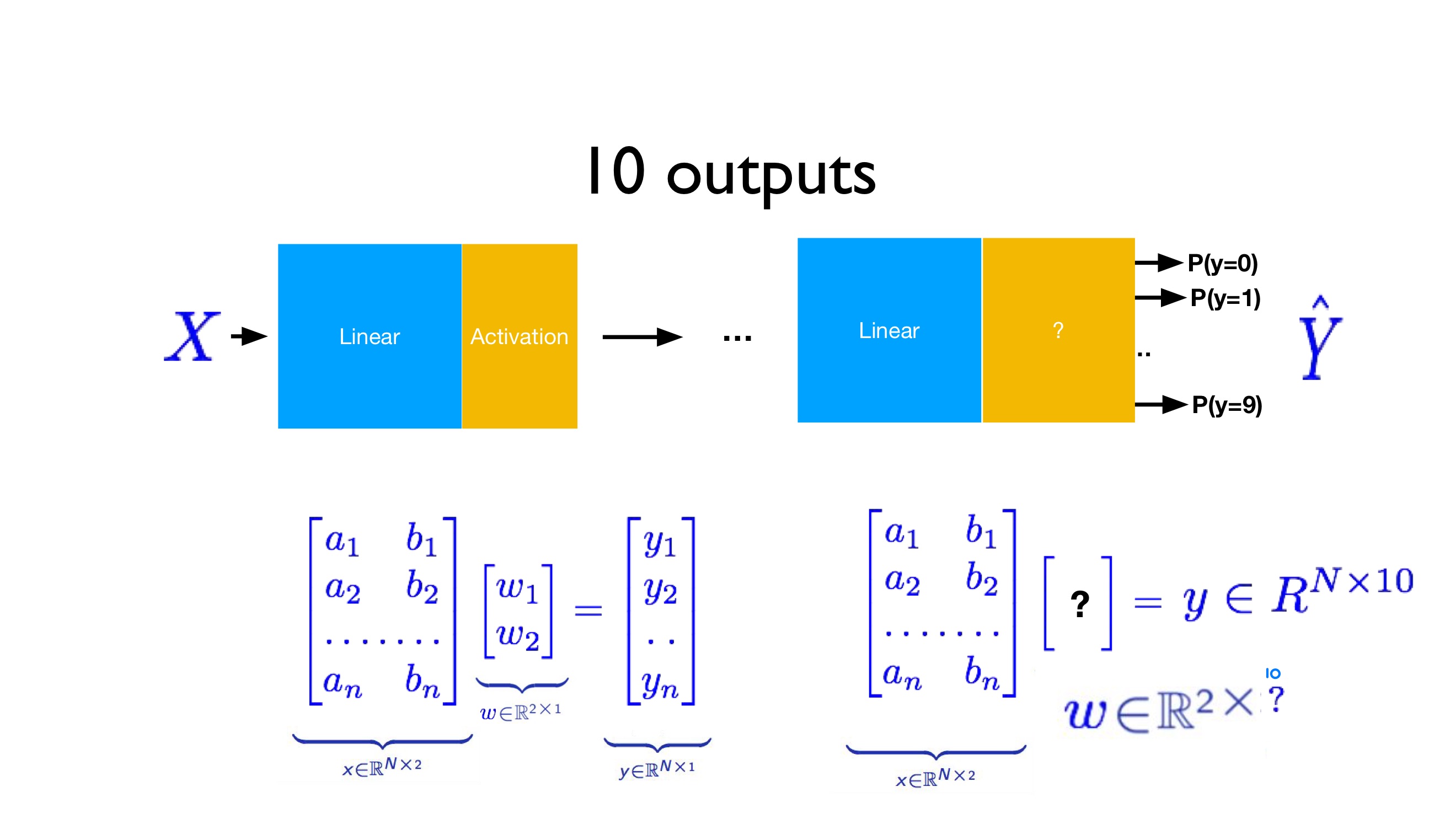
Label과 똑같은 수의 output을 갖기 위해 weight matrix는 #of input parameters x #of labels의 꼴을 갖습니다. 위의 예시의 경우 a와 b 2개의 parameter로 10개 label에 대해 예측을 진행하기 때문에 weight matrix는 2 x 10의 꼴이 됩니다. 10개의 output을 각 label에 속활 확률로 만들어주기 위해 softmax function을 사용합니다. Softmax function은 다음과 같습니다.
$\delta(z)_j = \frac{e^{z_j}}{\sum_{k=1}^{K}e^{z_k}}, for j = 1, ... , K$
주어진 input X에 대하여 linear operation을 거쳤더니 3개의 수를 출력했다고 가정합시다. 이 때, 이 3개의 수를 scores 혹은 logits이라고 부릅니다. 단순히 linear operation을 거친 것에 불과하기 때문에 이 3개의 수는 아무런 수나 될 수 있습니다. Logits에 대하여 softmax function을 적용하면 각 label에 속할 확률을 구할 수 있습니다. 확률을 구한 후 가장 높은 값에는 1을 취하고 나머지는 0을 취하는 one-hot encoding을 통해 y값을 구해줍니다. 1로 표시된 label이 해당 값이 속할 것이라 예측된 label입니다.
이후 cross entorpy를 통해 loss를 구해줍니다. Cross Entorpy는 다음과 같습니다.
$D(\hat{Y}, Y) = -Ylog\hat{Y}$
Loss는 다음과 같습니다.
L = $\frac{1}{N} \sum_{i}{}D(\hat{y_i}, y_i) = \frac{1}{N} \sum_{i}{}D(s(wx_i+b), y_i)$
새로워 보일 수 있지만, 이전 6과 설명 때 나왔던 cross entropy loss를 이진분류가 아닌 다항분류에도 사용될 수 있게끔 일반화 한 것에 불과합니다.
from torch import nn, tensor, max
import numpy as np
# Cross entropy example
# One hot
# 0: 1 0 0
# 1: 0 1 0
# 2: 0 0 1
Y = np.array([1, 0, 0])
#실제 y값, 첫번째 label에 속함
Y_pred1 = np.array([0.7, 0.2, 0.1])
#softmax function을 취한 후의 y값: y가 첫번째 label에 속할 확률이 제일 높습니다.
#예측이 잘 되었기 때문에 loss가 작은 것을 확인할 수 있습니다.
Y_pred2 = np.array([0.1, 0.3, 0.6])
#softmax function을 취한 후의 y값: y가 세번째 label에 속할 확률이 제일 높습니다.
#예측이 잘 되지 못했기 때문에 loss가 비교적 큰 것을 확인할 수 있습니다.
print(f'Loss1: {np.sum(-Y * np.log(Y_pred1)):.4f}')
print(f'Loss2: {np.sum(-Y * np.log(Y_pred2)):.4f}')
# Softmax + CrossEntropy (logSoftmax + NLLLoss)
loss = nn.CrossEntropyLoss()
#nn의 CrossEntropyLoss 불러와서 사용
# target is of size nBatch
# each element in target has to have 0 <= value < nClasses (0-2)
# Input is class, not one-hot
Y = tensor([0], requires_grad=False)
#Y는 0라벨에 속합니다. 이전처럼 one-hot value인 1, 0, 0으로 넣어준 것이 아니라
#그냥 해당 클래스를 바로 넣어주면 됩니다.
# input is of size nBatch x nClasses = 1 x 4
# Y_pred are logits (not softmax)
Y_pred1 = tensor([[2.0, 1.0, 0.1]])
Y_pred2 = tensor([[0.5, 2.0, 0.3]])
#CrossEntropyLoss() 안에 softmax도 내장이 되어있기 때문에 처음에 한 것 처럼
#softmax를 거친 값을 y_pred로 해줄 필요없이 logits을 바로 넣으면 됩니다.
l1 = loss(Y_pred1, Y)
l2 = loss(Y_pred2, Y)
print(f'PyTorch Loss1: {l1.item():.4f} \nPyTorch Loss2: {l2.item():.4f}')
print(f'Y_pred1: {max(Y_pred1.data, 1)[1].item()}')
print(f'Y_pred2: {max(Y_pred2.data, 1)[1].item()}')
# target is of size nBatch
# each element in target has to have 0 <= value < nClasses (0-2)
# Input is class, not one-hot
Y = tensor([2, 0, 1], requires_grad=False)
#첫번째는 3번째 label에, 두번째는 첫번째 label에, 세번째는 두번째 label에 속합니다.
# input is of size nBatch x nClasses = 2 x 4
# Y_pred are logits (not softmax)
Y_pred1 = tensor([[0.1, 0.2, 0.9],
[1.1, 0.1, 0.2],
[0.2, 2.1, 0.1]])
Y_pred2 = tensor([[0.8, 0.2, 0.3],
[0.2, 0.3, 0.5],
[0.2, 0.2, 0.5]])
l1 = loss(Y_pred1, Y)
#예측이 잘 되었기 때문에 loss가 작습니다.
l2 = loss(Y_pred2, Y)
#예측이 잘 되지 않았기 때문에 loss가 비교적 큽니다.
print(f'Batch Loss1: {l1.item():.4f} \nBatch Loss2: {l2.data:.4f}')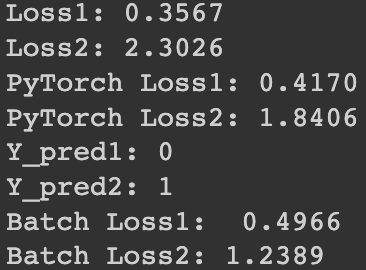

Input size가 28 x 28 = 784이기 때문에 input layer는 784, label이 0~9까지로 10개이기 때문에 output layer는 10이 됩니다. Input layer와 output layer 사이에 위치한 layer들은 hidden layers라 칭합니다. Input layer의 수와 output layer의 수는 고정되어있지만, hidden layer의 수와 층은 저희가 임의로 결정할 수 있습니다.
# https://github.com/pytorch/examples/blob/master/mnist/main.py
from __future__ import print_function
from torch import nn, optim, cuda
from torch.utils import data
from torchvision import datasets, transforms
import torch.nn.functional as F
import time
# Training settings
batch_size = 64
device = 'cuda' if cuda.is_available() else 'cpu'
print(f'Training MNIST Model on {device}\n{"=" * 44}')
#batch_size를 64로 설정하고 cuda 환경을 체크합니다.
#(GPU에 액세스 할 수 있는지 확인 후 available 하면 GPU를 그렇지 않으면 CPU를 사용합니다.)
#MNIST Dataset의 경우 크기가 작기 때문에 꼭 GPU를 사용하지 않아도 됩니다.
# MNIST Dataset
train_dataset = datasets.MNIST(root='./mnist_data/',
train=True,
transform=transforms.ToTensor(),
download=True)
test_dataset = datasets.MNIST(root='./mnist_data/',
train=False,
transform=transforms.ToTensor())
# Data Loader (Input Pipeline)
train_loader = data.DataLoader(dataset=train_dataset,
batch_size=batch_size,
shuffle=True)
test_loader = data.DataLoader(dataset=test_dataset,
batch_size=batch_size,
shuffle=False)
#train, test dataset에 대해 DataLoader를 제작합니다.
#nn.Module의 subclass인 class Net을 생성해줍니다.
class Net(nn.Module):
def __init__(self):
super(Net, self).__init__()
self.l1 = nn.Linear(784, 520)
self.l2 = nn.Linear(520, 320)
self.l3 = nn.Linear(320, 240)
self.l4 = nn.Linear(240, 120)
self.l5 = nn.Linear(120, 10)
#MNIST Dataset의 크기 28 x 28로 784이고, label이 0~9까지 10개이기 때문에
#첫번째 layer의 input은 784, 마지막 layer의 output은 10으로 고정
#나머지는 임의로 조정 가능합니다. 다만 n번째 input의 크기가 n-1번째 output의 크기와
#동일해야 합니다.
def forward(self, x):
x = x.view(-1, 784) # Flatten the data (n, 1, 28, 28)-> (n, 784)
#1개의 색깔과 가로 세로 28개씩의 pixel로 이루어진 MNIST dataset을
#view함수를 이용하여 (n, 1, 28, 28) -> (n, 784)로 바꾸어줍니다.
x = F.relu(self.l1(x))
x = F.relu(self.l2(x))
x = F.relu(self.l3(x))
x = F.relu(self.l4(x))
return self.l5(x)
#relu function은 sigmoid function을 대체한 activation function으로
#sigmoid function이 0과 1사이의 값을 가지기 때문에 backpropagation을 수행 시
#layer를 거치면서 gradient를 계속 곱해 0으로 수렴하게 되는 문제를 해결하기 위해
#등장했다고 합니다. ReLu는 입력값이 0보다 작으면 0으로, 0보다 크면 입력값을 그대로
#내보내는 함수입니다.
model = Net()
model.to(device)
#GPU로 보내주는 기능
criterion = nn.CrossEntropyLoss()
#기존에 사용했던 binary cross entropy loss를 torch.nn.BCELoss로 불러와 사용합니다.
#reduction = 'mean'이면 설명에 사용했던 대로 loss들의 평균을 사용하지만 reduction = 'sum'인 경우
#loss들의 총합을 사용합니다. default는 mean입니다.
optimizer = optim.SGD(model.parameters(), lr=0.01, momentum=0.5)
#SGD + Momentum
def train(epoch):
model.train()
for batch_idx, (data, target) in enumerate(train_loader):
data, target = data.to(device), target.to(device)
optimizer.zero_grad()
output = model(data)
loss = criterion(output, target)
loss.backward()
optimizer.step()
if batch_idx % 10 == 0:
print('Train Epoch: {} | Batch Status: {}/{} ({:.0f}%) | Loss: {:.6f}'.format(
epoch, batch_idx * len(data), len(train_loader.dataset),
100. * batch_idx / len(train_loader), loss.item()))
#train loader에 들어있는 학습에 필요한 데이터를 읽어와 학습을 진행하는 train 함수
def test():
model.eval()
test_loss = 0
correct = 0
for data, target in test_loader:
data, target = data.to(device), target.to(device)
output = model(data)
# sum up batch loss
test_loss += criterion(output, target).item()
# get the index of the max
pred = output.data.max(1, keepdim=True)[1]
#max값의 index를 pred로 받음
correct += pred.eq(target.data.view_as(pred)).cpu().sum()
#pred와 pred와 동일한 차원으로 형태를 변화시켜준 target.data의 element wise equality를
#체크해 맞으면 correct에 맞은 개수 저장해줍니다.
test_loss /= len(test_loader.dataset)
print(f'===========================\nTest set: Average loss: {test_loss:.4f}, Accuracy: {correct}/{len(test_loader.dataset)} '
f'({100. * correct / len(test_loader.dataset):.0f}%)')
#test_loader에서 데이터를 꺼내와 학습된 모델을 사용해 결과를 예측하는 test함수
#accuracy를 평가하는데에도 사용됩니다.
if __name__ == '__main__':
since = time.time()
#time.time()은 컴퓨터의 현재 시각을 구하는 함수
for epoch in range(1, 10):
epoch_start = time.time()
train(epoch)
m, s = divmod(time.time() - epoch_start, 60)
#divmod는 두 숫자를 인자로 전달 받아 첫번 째 인자를 나눈 몫과 나머지를 tuple형식으로 반환하는 함수
#m은 현재시각 - epoch_start한 시간을 60으로 나눈 몫, s는 나머지
#즉 m에는 분을, s에는 초를 저장합니다.
print(f'Training time: {m:.0f}m {s:.0f}s')
test()
m, s = divmod(time.time() - epoch_start, 60)
print(f'Testing time: {m:.0f}m {s:.0f}s')
m, s = divmod(time.time() - since, 60)
print(f'Total Time: {m:.0f}m {s:.0f}s\nModel was trained on {device}!')
#전체 데이터를 10번 반복하며 학습을 진행합니다. epoch이 늘어날수록 test set에 대한 loss도 감소하는 것을
#확인할 수 있습니다. 학습이 끝난 후의 accuracy는 97%로 매우 준수한 성능을 보이고 있습니다.
* 공부하면서 참고한 것들
** ReLU Function
https://www.youtube.com/watch?v=eMJm-Eoacdc&list=PLLhQgjrONLVFP1E7p2jWMMeM2FWUf2Qc7&index=5
** Momentum에 대한 설명, 다양한 gradient descent method에 대한 설명
https://hyunw.kim/blog/2017/11/01/Optimization.html
그림으로 보는 다양한 Optimization 기법들
딥러닝 모델의 optimization을 담당하는 gradient descent 알고리즘은 딥러닝의 핵심 중 하나입니다. 다양한 gradient descent 알고리즘들이 어떻게 발전해왔고, 각 장점은 무엇인지, 그리고 그 안에서 헷갈
hyunw.kim
** CPU와 GPU
https://velog.io/@euisuk-chung/CPU%EC%99%80-GPU
CPU와 GPU
CPU와 GPU의 차이에 대해 알아보도록 하겠습니다 :D
velog.io
'ML \ DL > PyTorch Zero To All' 카테고리의 다른 글
| PyTorch Lecture 11: Advanced CNN (0) | 2022.08.05 |
|---|---|
| PyTorch Lecture 10: Basic CNN (0) | 2022.07.26 |
| PyTorch Lecture 06: Logistic Regression (0) | 2022.07.13 |
| Pytorch Lecture 04: Back-Propagation and Autograd (0) | 2022.07.13 |
| PyTorch Lecture 03: Gradient Descent (0) | 2022.07.13 |