Binomial Distribution(이항분포)
이항분포를 설명하기 앞서 베르누이 시행(Bernoulli Trial)에 대해 알아야합니다. 베르누이 시행이란, 오직 2개의 결과만을 가지는 시행을 의미합니다. 베르누이 시행의 예시로는 동전 던지기(H/T), 신생아의 성별(남아/여아) 등이 있습니다.
성공확률이 $p$인 베르누이 시행을 $n$번 하였을 때, 성공 횟수 혹은 특정 사건의 발생 횟수 $x$를 확률변수로 하는 분포를 이항분포(Binomial Distribution)라 합니다. 이항분포함수는 다음과 같이 표현 가능합니다.
$p(x) = \binom{n}{x}p^x(1-p)^{n-x}$
$X\sim B(n, p)$
이를 확률변수 X가 시행횟수가 n, 성공확률이 p인 이항분포를 따른다고 합니다.
ex) 동전을 5번 던졌을 때 앞면이 3번 나올 확률
$\binom{5}{3}(0.5)^3(1-0.5)^{5-3} = \binom{5}{3}(0.5)^3(0.5)^{2} = 0.3125$
이항분포 $B(n, p)$를 따르는 X의 평균과 분산은 다음과 같습니다.
$E(X) = np, Var(X) = np(1-p)$
이항분포의 평균과 분산은 아래 방법을 따라 구할 수 있습니다.

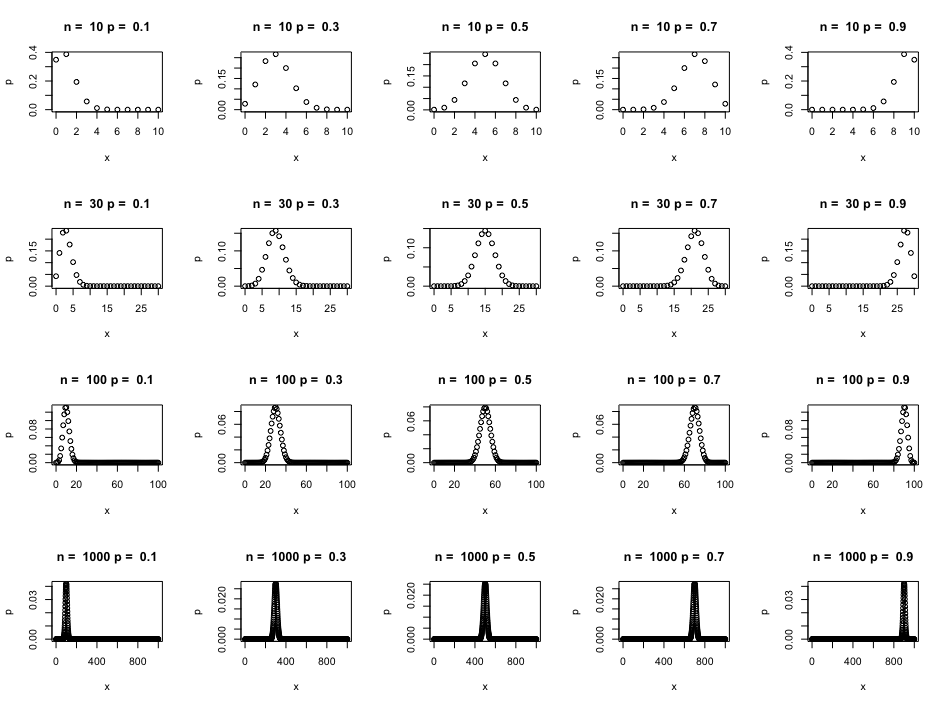
이항분포는 $n$이 충분히 크고, $p$가 너무 작거나 크지 않을 때, 정규분포에 근사하는 성질을 가지고 있습니다. 이를 R을 이용하여 표현해보았습니다.

Poisson Distribution(포아송분포)
다음은 포아송분포입니다. 단위시간 혹은 단위공간에서 일어나는 특정 사건의 횟수를 확률변수로 하는 분포를 포아송분포(Poisson Distribtuion)라 합니다. 포아송분포는 시행 횟수(n)이 굉장히 크고, 성공 확률(p)가 매우 작은 이항분포의 특수한 경우입니다.(일반적으로, n\geq 20이고 p\leq 0.05 포아송분포의 함수는 다음과 같이 정의됩니다.
$f(x) = \frac{\lambda^xe^{-\lambda}}{x!}$
확률변수 X가 모수가 \lambda인 포아송분포를 따르는 경우 다음과 같이 표현하기도 합니다.
$X \sim Poisson(\lambda)$
포아송분포에 대한 이해를 돕기 위해 간단한 예시를 들어보겠습니다.
하루(6시간)알바하면서 주문 받는 카라멜 마끼아또의 수
이 때, 시행 횟수는 제가 알바를 하는 모든 순간이 됩니다. $n$을 정의할 수 없습니다. 카라멜 마끼아또를 주문 받을 확률 $p$ 또한 작다는 것은 알지만 뭐라 정의하기 힘듭니다. 하지만 하루(6시간) 알바하면서 만드는 카라멜 마끼아또의 평균 잔수, 즉 $np$는 정의할 수 있습니다. 포아송분포에서는 이 $np$를 $\lambda$라 정의합니다. 포아송분포를 이항분포의 특수한 경우라고 소개한 만큼, 이항분포로부터 포아송분포를 유도해보았습니다.

포아송분포의 평균과 분산은 다음과 같습니다.
$E(X) = \lambda, Var(X) = \lambda$
포아송분포의 평균과 분산은 다음 과정을 따라 구할 수 있습니다.

다시 예시로 돌아가보겠습니다.
ex) 하루(6시간) 알바하면서 주문 받는 카라멜 마끼아또가 평균 2잔일 때, 4잔을 만들 확률은?
$\lambda = 2, x =4$, $\frac{2^4e^-2}{4!} = 0.09$
Exponetial Distribution(지수분포)
포아송분포에서 들었던 카라멜 마끼아또 예제를 이어서 사용하겠습니다. 카라멜 마끼아또를 주문 받을 때까지 걸리는 기간이 X이하일 확률은 얼마가 될까요? 좀 더 일반화시켜, 단위시간, 단위공간 당 평균발생횟수를 $\lambda$라 할 때, 사건이 발생할 때까지 걸리는 시간이 X이하일 확률은 얼마일까요? 이 질문의 답을 아래 그래프의 색칠한 면적과 일치시켜주는 함수 $f(x)$가 지수분포(Exponential Distribution)함수입니다.

특정 확률변수 $X$가 지수분포를 따르는 경우, $X \sim Exp(\lambda)$와 같이 표현합니다.
다시 예시로 돌아와서, 카라멜 마끼아또 첫 주문을 받기까지 걸리는 시간이 3일 이하일 확률은
어떻게 될까요? 걸리는 시간이 3일 이하일 확률이 구하기 위해서는 전체 확률 1에서 여사건인 3일동안 주문이 안 들어올 확률을 빼주면 됩니다. 하루동안 카라멜 마끼아또 주문이 없을 확률은 $p(0) = \frac{2^0e^{-2}}{0!} = e^-2$입니다. 따라서 3일동안 주문이 안 들어올 확률은 $e^{-2}e^{-2}e^{-2} = e^{-2\times3}$이 됩니다.
카라멜 마끼아또 첫 주문을 받기까지 걸리는 시간이 3일 이하일 확률은
$P(0\le x \le3) = \int_{0}^3 f(x)dx = 1- e^{-2\times3}$
으로 구할 수 있습니다.
평균을 $\lambda$, 기간을 $X$로 바꾸어 일반화해주면
$P(0\le x \le X) = \int_{0}^X f(x)dx = 1 - e^{-\lambda x}$로 표현할 수 있습니다.
마지막으로, 양분을 미분해주면, 저희가 원하는 지수분포함수인
$f(x) = \lambda e^{-\lambda x}$를 구할 수 있습니다.
지수분포의 평균과 분산은 다음과 같습니다.
$E(X) = {1 \over \lambda}, Var(X) = {1 \over \lambda^2}$
지수분포의 평균과 분산은 다음 과정을 따라 구할 수 있습니다.
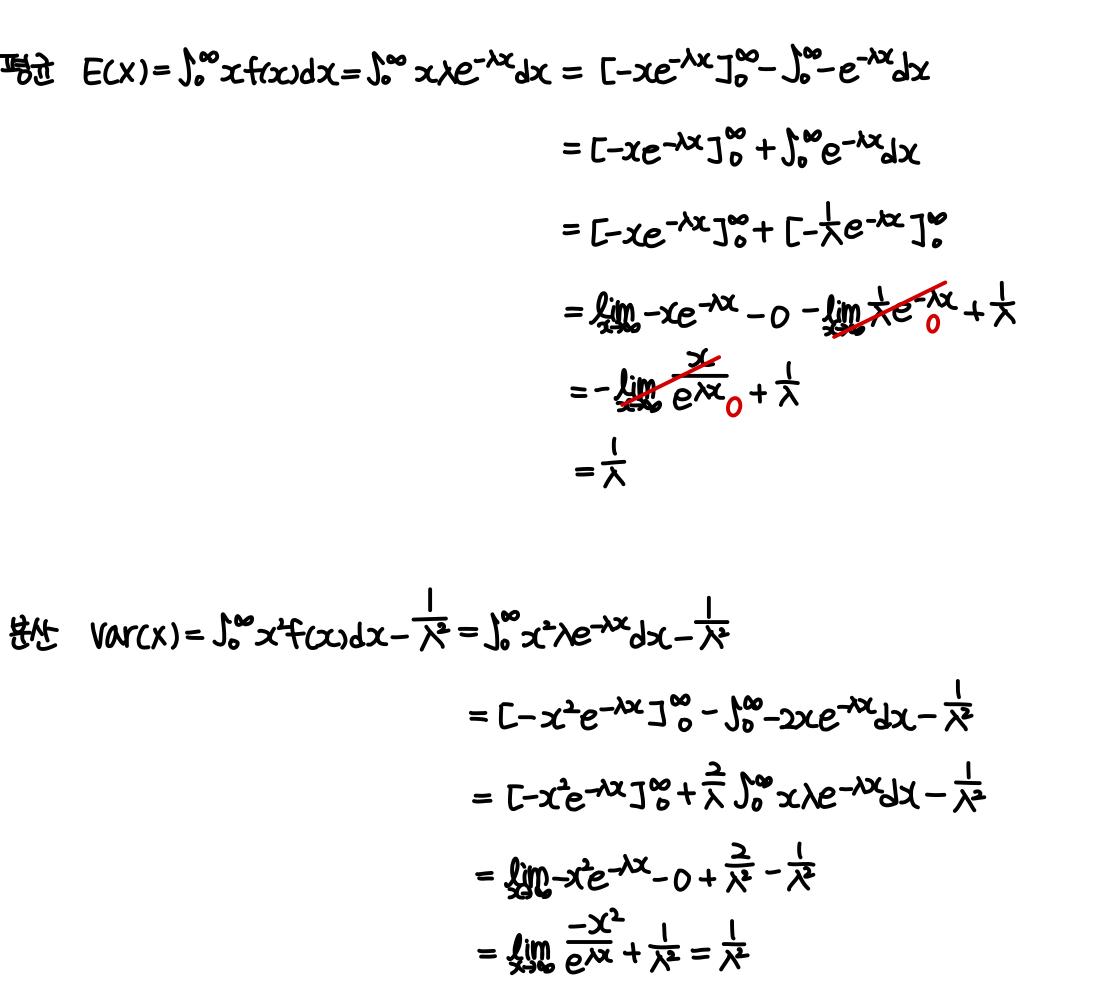
이해를 돕기 위해 예제를 하나 준비해보았습니다. 카라멜 마끼아또 주문이 평균 10분마다 들어온다고 할 때, 다음 주문까지 10~20분 사이로 기다릴 확률은 어떻게 될까요? 이 예제에서 주의하셔야할 점은, 저희에게 주어진 건 평균 주문시간이지, 평균 주문횟수가 아니라는 점입니다. 따라서 $\lambda$를 무턱대고 10으로 사용하시면 안됩니다. 10분에 한 건 주문이 들어오는 것이므로, 단위시간을 1시간으로 한다고 하면, $\lambda$는 6이 됩니다. 10분에서 20분도 이제 시간 단위로 1/6시간에서 1/3시간으로 사용해주어야할 것입니다.
$P({1 \over 6} \le X \le {1 \over 3}) = \int_{{1 \over 6}}^{1 \over 3} \lambda e^{-\lambda X}dx = -e^{-2} + e^{-1} = 0.233$
지수분포를 사용하는 경우 대부분 예제와 같이 적분 과정을 거치기 때문에 지수분포의 누적분포함수의 꼴인 $1 - e^{-\lambda X}$를 기억하고 있는 것이 도움이 될 수 있습니다.
지수분포함수의 중요한 특성 중 하나가 무기억성(Memorylessness property of the exponential PDF)입니다. 무기억성은 다음 특성을 의미합니다.
$P(X \ge s + t | X \ge t) = P(X > s)$
LHS는 이미 t만큼의 시간이 지났을 때, s만큼 시간이 추가로 흐른 후 사건이 발생할 확률을 의미합니다. RHS는 s만큼 시간이 흘렀을 때 사건이 발생할 확률을 의미합니다. 예를 들면, 오늘 구매하여 사용한 노트북이 2년 후 고장이 날 확률이, 동일한 노트북을 고장 없이 3년 사용했을 때, 다시 2년 후(총 사용년수는 5년이 됩니다)에 고장날 확률과 같다는 것입니다.
지수분포의 무기억성은 다음과 같이 유도 가능합니다.

Chi-Square Distribution(카이제곱분포)
카이제곱분포(Chi-Square Distribution)은 각각 독립인 표준정규분포인 확률변수 $Z_i$의 제곱의 합이 따르는 확률분포입니다.
$Z_1^2 + Z_2^2 + \dots + Z_p^2 \sim \chi^2_{(p)}$
이를 자유도가 p인 카이제곱분포를 따른다라고 읽습니다.
교재에서는 카이제곱분포를 카이제곱 검정통계량 $\chi^2 = \sum_{i=1}^{p} {(o_i - e_i)^2 \over e_i}의 확률분포로 설명하고 있습니다. 이 때 $o_i$는 observed value이고, $e_i$는 귀무가설($H_0$: 변수들은 서로 독립이다.) 하에서의 expected value입니다. $o_i$와 $e_i$ 사이 차이가 작으면 통계량이 작아지고, p-value가 커지므로 귀무가설을 기각하지 못하게 됩니다. 반대로, $o_i$와 $e_i$간의 차이가 크면, 통계량이 커지고, p-value가 작아져 귀무가설을 기각, 두 변수들이 서로 관계가 있다고 볼 수 있습니다. 예시로는 성별과 사후세계에 대한 믿음이 관계가 있는지 등이 있을 수 있습니다. 다음 단원에서 다양한 testing에 대해 다루는 것 같으니, 검정통계량에 대해서는 이 정도만 설명하고 넘어가도록 하겠습니다.
카이제곱분포의 경우, $\alpha = {p \over 2}, \beta = 2$인 감마분포의 특수한 경우인데, 감마분포에 대해 따로 다루지 않았기 때문에, 분포함수의 유도과정은 생략하였습니다.
카이제곱분포함수는 다음과 같이 표현됩니다.
$f(x, p) = {1 \over 2^{p/2}\Gamma({p \over 2})}x^{{p \over 2}-1}e^{{-x \over 2}}, x > 0$
카이제곱분포의 평균과 분산은 각각 자유도, 그리고 자유도 x 2 입니다.
$E(X) = p, Var(X) = 2p$
카이제곱분포의 평균과 분산은 다음과 같이 유도됩니다.

카이제곱분포의 특성
1. 표준정규분포의 제곱값의 합이 따르는 확률분포이므로 항상 양수값만 지닙니다.
2. 자유도 p에 따라 분포의 형태가 변하며, 자유도가 커질수록 오른쪽으로 치우친 형태에서 종 모양으로, 정규분포에 근사하게 됩니다.

F-Distribution(F 분포)
마지막으로 F 분포입니다. 자유도가 $p_1$인 카이제곱분포를 따르는 확률변수 $X_1$과 자유도가 $p_2$인 카이제곱분포를 따르는 확률변수 $X_2$가 존재할 때, F통계량을 ${X_1/p_1 \over X_2/p_2}$이라 정의하겠습니다. 이 F통계량이 따르는 분포가 자유도가 $p_1$, $p_2$인 F 분포(F-Distribution)이 됩니다. 수식으로 표현하면 다음과 같습니다.
Let $X_1 \sim \chi^2(v_1), X_2 \sim \chi^2(v_2)$
$F = {X_1/p_1 \over X_2/p_2} \sim F(v_1, v_2)$
F분포는 주로 두 집단의 분산을 비교하기 위해 사용됩니다. 이 때, 나누어진 값을 사용하기 때문에, F값이 1이면 두 분산에 차이가 없는 것이고, F값이 1이 아니라면 두 분산에는 차이가 있는 것이 됩니다.
F분포의 분포함수입니다.
$f(x) = {\Gamma({v_1 + v_2 \over 2})({v_1 \over v_2})^{{v_1 \over 2}}x^{{v_1 \over 2} - 1} \over \Gamma(v_1/2)\Gamma(v_2/2)(1+{v_1 \over v_2}x){v_1 + v_2 \over 2}}, x \ge 0$
F분포의 평균과 분산입니다.
$E(X) = {v_2 \over v_2 -2}, Var(X) = {2v_2^{2}(v_2+v_1-2) \over v_1(v_2 -2)^{2}(v_2-4)}$
F분포는 분포에 대한 엄청난 이해가 요구되기보다는, 후에 나올 검정에서 훨씬 유의미하게 다뤄지기 때문에, 여기서는 간단히 소개하는 정도로만 넘어가도록 하겠습니다.
긴 글 읽어주셔서 감사합니다.